Mathematician manqué?
Aaron Haspel has selected me as his Ideal Reader: 'a kindred spirit, not a doppelgänger'—this is because, apparently, I am 'literary but [have] mathematics as well, sympathetic but critical'. (Haspel remarks that he is 'too poor a linguist' to be my ideal reader, which is doubtless code for 'he finds all the language stuff boring'.) Well, my readers know all about the literary, but how about the maths, the 'tique? There's a good reason that I'm not a mathematician, despite my leanings in that direction during my teenage years. I was never first rank—it wasn't just that I didn't invent modular arithmetic at age 19—hell, I couldn't even calculate Euler's constant to 15 decimal places at age 17—it was that I made elementary errors at inopportune moments.
One such moment would prove decisive. I was sitting the M3 [third mechanics] final paper of my Further Maths A-Level, when I came across a problem of angular velocity and circular motion down a slope. It was basic stuff, and I'd seen similar problems dozens of times before: something like a snowball (taken as a non-elastic sphere) rolling down the top of an igloo.
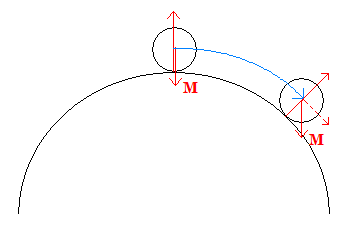I don't recall the specifics now. But it must have involved elementary formula-plugging and vector-resolution, always the dullest part of mathematical physics. Anyway, there is one thing that you must remember when working on circular motion—the direction of velocity is not the same as the direction of acceleration. In this case, the latter is just straight down with gravity (M), while the former is tangential to the plane of the igloo—here marked with a dotted line, the resolution of the gravitational force and the force of the surface against the ball.
I blanked on this.
So I got a C on the paper, and a B on the class—thus missing an A by about 3 points off 720. It may not sound like much, but when you're swimming with geniuses to whom this stuff is a piss in the park, it makes all the difference. I think it was this moment that ultimately led to me leaving mathematics (and hence physics) in school, and becoming the littérateur you read today. One doesn't have to be a Perec or a Pynchon, therefore, to see in the above figure an icon of my fall from mathematical grace. Words had always been good to me—ever since I was the only child in my class, age 8, to know that the opposite of 'transparent' was 'opaque'—thanks, MacPaint!—but numbers. . . well, I'm not afraid of them, but I could never really have been a contender.
One such moment would prove decisive. I was sitting the M3 [third mechanics] final paper of my Further Maths A-Level, when I came across a problem of angular velocity and circular motion down a slope. It was basic stuff, and I'd seen similar problems dozens of times before: something like a snowball (taken as a non-elastic sphere) rolling down the top of an igloo.
I don't recall the specifics now. But it must have involved elementary formula-plugging and vector-resolution, always the dullest part of mathematical physics. Anyway, there is one thing that you must remember when working on circular motion—the direction of velocity is not the same as the direction of acceleration. In this case, the latter is just straight down with gravity (M), while the former is tangential to the plane of the igloo—here marked with a dotted line, the resolution of the gravitational force and the force of the surface against the ball.I blanked on this.
So I got a C on the paper, and a B on the class—thus missing an A by about 3 points off 720. It may not sound like much, but when you're swimming with geniuses to whom this stuff is a piss in the park, it makes all the difference. I think it was this moment that ultimately led to me leaving mathematics (and hence physics) in school, and becoming the littérateur you read today. One doesn't have to be a Perec or a Pynchon, therefore, to see in the above figure an icon of my fall from mathematical grace. Words had always been good to me—ever since I was the only child in my class, age 8, to know that the opposite of 'transparent' was 'opaque'—thanks, MacPaint!—but numbers. . . well, I'm not afraid of them, but I could never really have been a contender.
9 comments:
Ah yes. But do you have the ideal reader's ideal insomnia, too?
Funny, I too am a mathematician manqué. I read Men of Mathematics in high school and was sure I was going to be another Euler or Poincaré; I cruised through my advanced classes with ease and entered college a math major. Then I hit the wall: it wasn't easy any more, and I got sick of all the calculus they kept insisting I take (I was never interested in anything with practical applications), and I migrated over to the languages department.
John: unfortunately, yes.
Steve: here's to magpietism! Curious though that your interest in maths (ie. not in the practical) should be the opposite of your linguistic interest...
> "(I was never interested in anything with practical applications), and I migrated over to the languages department."
Fantastic! I'm so pleased to know that my number-one passion is just as inapplicable as I desperately hoped it would be.
Tut-tut--that's no sort of attitude for an exegete of the Tanakh, Simon!
Curious though that your interest in maths (ie. not in the practical) should be the opposite of your linguistic interest.
But no! It is the opposite of the opposite! When I was in Japan, I studied French and Latin. When I was in Argentina, I studied Russian. When I got into linguistics, did I specialize in something practical, like English As a Foreign Language or even Transformational Grammar (which, however unconnected with reality, would have pretty much guaranteed me a job)? No, I studied Indo-European, a discipline that had been on a downward track (in terms of widespread scholarly enthusiasm) for a century or so. Had I gone on to get my PhD, I would have had to wait for one of the three or four Indo-Europeanists in the country to die and join the vicious swarm of fellow useless degree-holders competing for their jobs (like applicants for NYC apartments recently vacated by freshly dead tenants).
After spending all that money and not getting a PhD, do I use it to make money now? No, I run a damn blog. I earn my living from my knowledge of the picky points of spelling and grammar, absorbed from a lifetime of reading (with no thought of practical value -- if anyone had told me "read lots of books and you can get a job as an editor," I would have resented the whole idea and probably taken up something even more useless, like Zen).
NEVER accuse me of practicality!
Okay, point taken--I was thinking along the lines of 'theoretical linguistics has no real point except within the academic world, while actually learning languages helps you to read, communicate, edit, etc.'
Steve, your Russian is practical (I suspect you can speak fluently, just shy away from it). I suspect if some medieval German scholast would suddenly turn on your doorstep you will easily slip into conversational Latin with him.
I also think other, practical, people did a scandalously bad job of appropriating your impractical body of knowledge; why, you could spy for all members of UN!
I suspect if some medieval German scholast would suddenly turn on your doorstep you will easily slip into conversational Latin with him.
Now, that would be a good use of the Latin good Brother Auger drilled into me back at St. Mary's!
...why, you could spy for all members of UN!
Say, now there's an idea... But no, B. would never move back to NYC. Another million-dollar idea down the drain!
Post a Comment