Mathematician manqué?

Aaron Haspel has selected me as his Ideal Reader: 'a kindred spirit, not a doppelgänger'—this is because, apparently, I am 'literary but [have] mathematics as well, sympathetic but critical'. (Haspel remarks that he is 'too poor a linguist' to be my ideal reader, which is doubtless code for 'he finds all the language stuff boring'.) Well, my readers know all about the literary, but how about the maths, the 'tique? There's a good reason that I'm not a mathematician, despite my leanings in that direction during my teenage years. I was never first rank—it wasn't just that I didn't invent modular arithmetic at age 19—hell, I couldn't even calculate Euler's constant to 15 decimal places at age 17—it was that I made elementary errors at inopportune moments.

One such moment would prove decisive. I was sitting the M3 [third mechanics] final paper of my Further Maths A-Level, when I came across a problem of angular velocity and circular motion down a slope. It was basic stuff, and I'd seen similar problems dozens of times before: something like a snowball (taken as a non-elastic sphere) rolling down the top of an igloo.
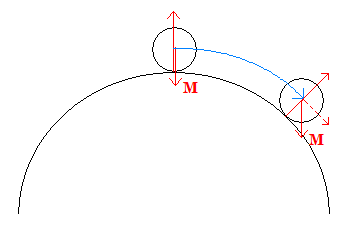I don't recall the specifics now. But it must have involved elementary formula-plugging and vector-resolution, always the dullest part of mathematical physics. Anyway, there is one thing that you must remember when working on circular motion—the direction of velocity is not the same as the direction of acceleration. In this case, the latter is just straight down with gravity (M), while the former is tangential to the plane of the igloo—here marked with a dotted line, the resolution of the gravitational force and the force of the surface against the ball.

I blanked on this.

So I got a C on the paper, and a B on the class—thus missing an A by about 3 points off 720. It may not sound like much, but when you're swimming with geniuses to whom this stuff is a piss in the park, it makes all the difference. I think it was this moment that ultimately led to me leaving mathematics (and hence physics) in school, and becoming the littérateur you read today. One doesn't have to be a Perec or a Pynchon, therefore, to see in the above figure an icon of my fall from mathematical grace. Words had always been good to me—ever since I was the only child in my class, age 8, to know that the opposite of 'transparent' was 'opaque'—thanks, MacPaint!—but numbers. . . well, I'm not afraid of them, but I could never really have been a contender.